
Arriva sempre un momento in cui la misconosciuta ricerca innovativa riesce a compiere il definitivo balzo verso gli onori. Per le moderne teorie della finanza questo salto avvenne grazie a due personaggi che ci vorrebbe la fantasia di un Pirandello a mettere assieme.
All’inizio degli anni 70 i mercati delle opzioni e dei contratti a termine, benchè esistenti da decenni (ricordo che nel 1900 a Parigi Bachelier iniziò proprio studiandoli), erano ancora non regolamentati e le contrattazioni avvenivano off the market via telefono o telescrivente fra due mediatori senza un clearing regolamentato.
Da decenni menti brillanti davano craniate sui muri per individuare una equazione che determinasse il prezzo di questi diritti di opzione, ma invano. L’idea di partenza, che cioè si dovesse in qualche modo sapere il prezzo finale, era semplicemente fuordeviante.
Quel tale della Arthur D.Little, J.Treynor che abbiamo già incontrato con il Capm, aveva belle idee al proposito ed era riuscito a affascinare un collega, Fisher Black, un ingegnere con specializzazione in matematica applicata che si mise sul problema di buon buzzo.
Comprese che il dilemma andava risolto con le sole informazioni che i broker possedevano: il prezzo attuale del titolo sottostante, la scadenza del contratto a premio e il prezzo di esercizio a cui poter comprare il contratto. Alla fine degli anni 60 elaborò una equazione differenziale così complicata che dopo vari affannati tentativi di risolverla decise di interrompere le sue pene e schiarirsi la mente occupandosi d’altro. Nel frattempo avrebbe fatto una capatina al MIT dove aveva delle conoscenze.

A quell’epoca il MIT era il crogiuolo delle migliori teste del pianeta, raccolte intorno a Paul Samuelson, Franco Modigliani, Solow e Cootner, quest’ultimo un vero hooligan della random walk theory. Questi erano soliti trovarsi ogni martedì sera, insieme con i rispettivi assistenti e altri cattedratici, a discutere delle novità economiche e finanziarie. Fu qui che Black conobbe il giovane economista canadese Myron Scholes, nativo della regione più a nord del paese dove il padre si era trasferito seguendo la caccia all’oro.
La coppia doveva sembrare male assortita per molte ragioni: allampanato, magro e riservato tanto da passare per taciturno lo smemorato americano; scontroso, lunatico e dal carattere burbero quanto prodigiosa era la memoria il canadese.
Si misero subito sulla strana e poco intuitiva equazione di Fisher e qualche aiuto in matematica lo ebbero da un altro personaggio degno di un quadro cubista, l’assistente di Samuelson, Robert C.Merton, un ingegnere specializzato in matematica al Caltech ma con l’ossessione compulsiva per la borsa: si alzava ogni mattina e correva al primo ufficio di brokeraggio per l’apertura delle negoziazioni che seguiva diligentemente sul nastro della telescrivente. Dopo aver scommesso per un paio d’ore, andava a lezione.
I tre capirono presto che ciò che fa la differenza per il mediatore nel determinare il prezzo dell’opzione è la variabilità del prezzo del titolo sottostante. Se un titolo ha un prezzo molto stabile, allora sarà ben difficile che i contratti a termine out of the money abbiano valore per qualcuno. Se invece il titolo ha variazioni abbastanza ampie, allora presto o tardi potrebbe diventare in the money e giustificare l’attivazione dell’opzione. E così procedendo arrivarono ad una formula risolutiva.
Non ho l’arroganza di affermare che sarei capace di spiegarla intuitivamente. Chi fosse interessato, una buona ma semplicistica spiegazione la può trovare su wikipedia cercando il paragrafo sulla risistemazione che Black ne fece nel 1976. Altrimenti si becca la spiegazione sotto
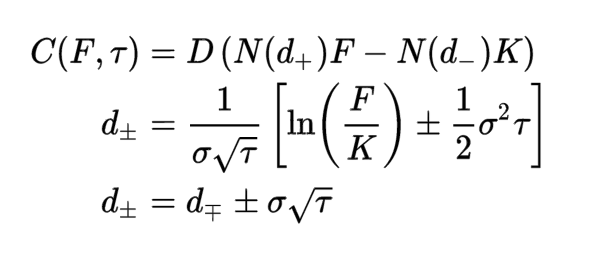
Una opzione call C(F, t) scambia alla scadenza denaro contro il titolo sottostante; essa si può scomporre in due opzioni binarie, una call “titolo o niente” (N(d+)F) e un’altra call “denaro o niente”(N(d-)K): la prima consegna il titolo senza scambio di denaro, la seconda consegna denaro senza scambio di titoli. d+ e d- sono valori casuali determinati come indicato sotto l’equazione, per i quali si assume distribuzione normale. Il valore della call option è pari alla differenza dei due termini attualizzati al fattore di sconto D. Ci avete capito poco immagino, non me ne vogliate.
I tre amici, per arrivarci, avevano fatto alcune ipotesi di partenza per permettere al modello di funzionare. Alcune delle prime, piuttosto ingombranti, ipotesi furono sistemate col tempo: qualche anno dopo la pubblicazione, Merton costruì un modello che eliminava le ipotesi di assenza di frizioni nel mercato, assenza di tassazione e di costi di transazione.
Ma ne rimaneva comunque una bella tosta: che le variabili casuali dell’equazione seguissero distribuzioni normali gaussiane indipendenti e identicamente distribuite e che i prezzi avessero variazioni continue, in altre parole che non facessero salti.
Ma si sa: se ci si fermasse ad ogni dubbio, non si rischierebbe e non si rosichierebbe nulla.
Forti della loro formula i tres amigos la applicarono subito al mercato e individuarono presto delle opzioni convenienti. In particolare ne trovarono una e si fiondarono a comprarne a manate (dannato entusiasmo giovanile: occhio al rischio, diversificate ragazzi!!) Caso volle che da lì a poco una società finanziaria annunciasse una offerta sui titoli di questa società causandone una riduzione del valore.
Ci rimisero un bel pacco di soldi, ma questo non li scoraggiò: la formula aveva individuato bene i casi anomali e quindi era forte.
I nostri eroi decisero allora per la pubblicazione, ma anche loro dovettero penare perchè il loro lavoro venisse riconosciuto: diverse riviste lo trovarono troppo specialistico e lo rifiutarono. Fu solo per l’intervento di qualche potente amico (Fama e Merton) che ottennero una pubblicazione nel 1973. Ma sarebbero stati ripagati.
Da lì a qualche anno tutti gli operatori parlavano per beta, delta, gamma e altri greeks che indicavano i parametri delle principali formule, dal Capm a quella delle opzioni.
A molti sembrava che ormai il cielo, finora oscuro o nebbioso, si rischiarasse. Almeno fino al crollo borsistico del 19 ottobre 1987. Malgrado questo piccolo incidente di percorso, nel 1997 la formula valse a Scholes e Merton il Nobel (Black era morto da qualche anno, e Scholes lesse in suo onore un elogio funebre).
Forse il Nobel sarebbe stato meglio darglielo molto prima, visto che l’anno successivo Scholes e Merton fecero naufragio con l’hedge fund LTCM di cui erano cofondatori, aggravando uno dei tumulti finanziari più grandi della storia, almeno fino a quel dì, causato dalla moratoria russa sul debito e dal downgrading di quello italiano, sui quali LTCM era pesantemente esposto, una crisi che arrivò persino a lambire la gestione dei fondi pensione della Banca d’Italia.
E sì che in LTCM sedevano alcuni dei ricercatori universitari più accreditati, tanto che fu definito, senza scherzo, il miglior dipartimento di finanze al mondo.
Perchè LTCM naufragò, e perchè la formula dei derivati cominciò a imbarcare acqua?
Facciamo un passo di lato: una delle applicazioni più usate della idea di Black e Scholes è la c.d.”superficie di volatilità”, che altro non è che un grafico tridimensionale di come si ampliano e si riducono le oscillazioni dei prezzi al variare dei termini di ciascun contratto. Stando alla teoria tradizionale questo lavoro di analisi dovrebbe essere di una noia mortale: la superficie dovrebbe presentarsi piatta come una tavola, e invece è una figura complessa fatta di picchi e avallamenti in tumultuosa modifica. Molti guadagni si fanno cercando di prevedere correttamente come sfruttare i potenziali arbitraggi impliciti.
Cosa c’è che non va nella formula? Beh, su questo punto si sono raccolte negli anni la maggior parte delle evidenze: le variazioni dei prezzi non sono una variabile continua, tanto per iniziare. Forse siamo implicitamente portati a pensarlo guardando un grafico standard, ma se lo cambiassimo adottandone uno a candele ci accorgeremmo che i prezzi fanno salti, molto spesso di magnitudine trascurabile, ma più spesso di quanto la teoria preveda ne fanno di altezze significative. E questo vale sia se considerassimo un periodo lungo, sia nel corso della giornata di contrattazioni.
Basta aprire il giornale per vedere con i nostri occhi cosa da un giorno all’altro può accadere se il cap del franco svizzero viene rimosso, oppure vincono referendum anti europa, oppure un paese riceve un ammonimento da Francoforte per i propri conti pubblici (Italia agosto 2011) o li riceve una banca in particolare (MPS, giorni nostri).
Alla faccia della continuità, i prezzi si muovono selvaggiamente, spesso a sorpresa, in barba ai nostri maldestri tentativi di imbrigliarli in formule che pur difficilissime ai nostri occhi sono ancora puerili rispetto alla complessità della realtà.
